Les opérations logiques, ou portes logiques, sont les opérations les plus basiques que l’on peux réaliser sur un bit. Nous allons voir ensemble les différentes portes logiques utilisées par notre processeur. Puis nous verrons que l’on peux combiner plusieurs portes logiques ensembles pour faire des opérations plus complexes, comme des additionneurs par exemple.
Pour bien comprendre cet article, il faut bien maitriser les notions de binaire et de bit. Pour rappelle, votre ordinateur fonctionne avec le langage binaire qui est composé de seulement 2 caractères, le ‘0’ et le ‘1’. On stock cette information dans des bits. Un bit peu donc contenir l’information ‘1’ ou ‘0’. D’un point de vue électronique, les bits correspondent à des transistors.
Finalement, dans l’article sur le binaire, nous avons vue comment stocker et interpréter le binaire, nous allons maintenant voir comment le traiter pour réaliser des opérations basiques que réalise, notamment, notre processeur. Comme pour les bits, les portes logiques sont, d’un point de vue électronique, composés de transistors.
Une porte logique prend en entré un ou plusieurs bits et génère en sortie un bit de résultat. Ce résultat dépend de l’état des bits en entrée et du type de la porte logique. On représente alors l’ensembles des valeurs d’entrée possibles et leur résultats en sortie dans un tableau nommé la table de vérité. Attention, il existe deux représentations pour chaque porte logique, une Américaine et une Européenne 😉
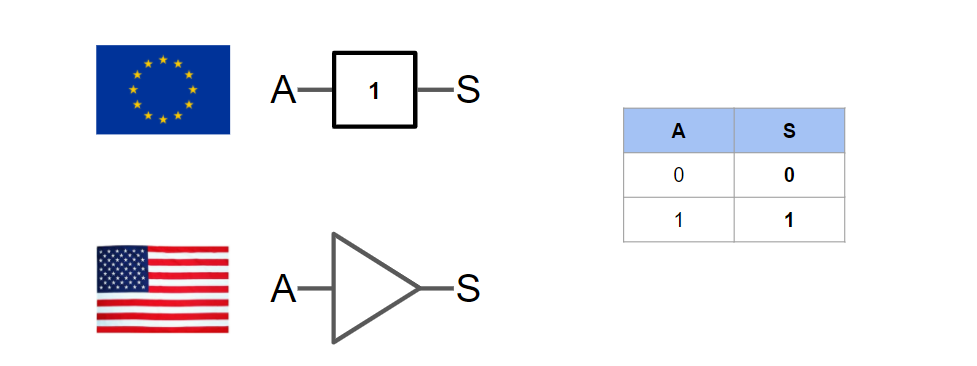
Portes logiques une entrée
La porte logique YES (oui)
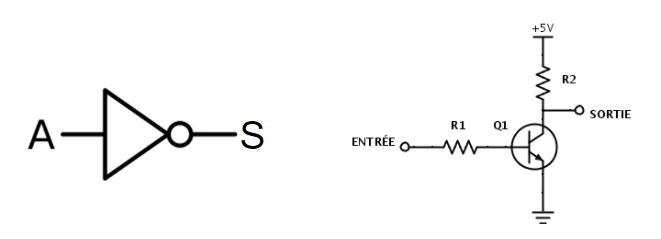
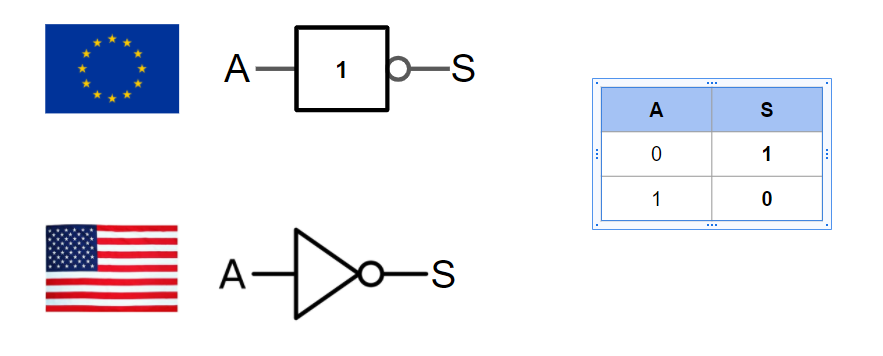
La porte logique NOT (non)
La porte NOT donne en sortie, l’inverse de la valeur du bit d’entrée. Donc si en entrée nous avons un ‘1’ alors en sortie nous allons avoir un ‘0’.
Les portes logiques deux entrées
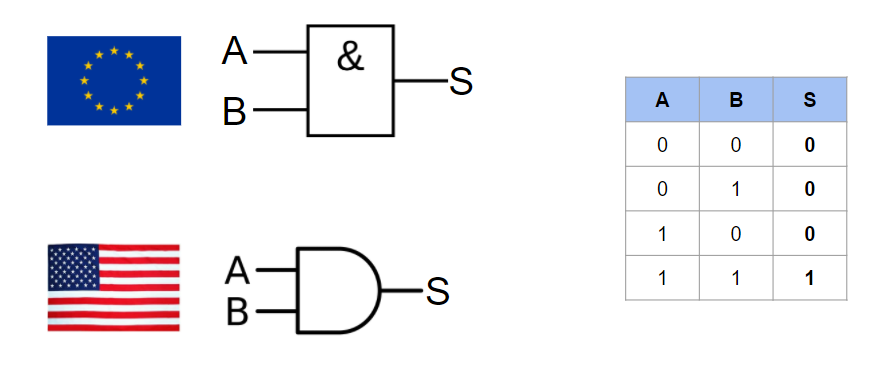
La porte logique AND (et)
la porte logique AND, ou ET en Français, porte bien sont nom car elle vas générer un ‘1’ en sortie si et seulement si les deux bits en entrées sont égaux à ‘1’. Dans les autres cas, nous avons donc un ‘0’ en sortie.
La porte logique OR (ou)
La porte OR (ou en Français), génère en sortie un ‘1’ si au moins un des bits en entrée est à ‘1’. Nous avons donc un ‘0’ en sortie, si et seulement si les deux bits en entrée sont à ‘0’.
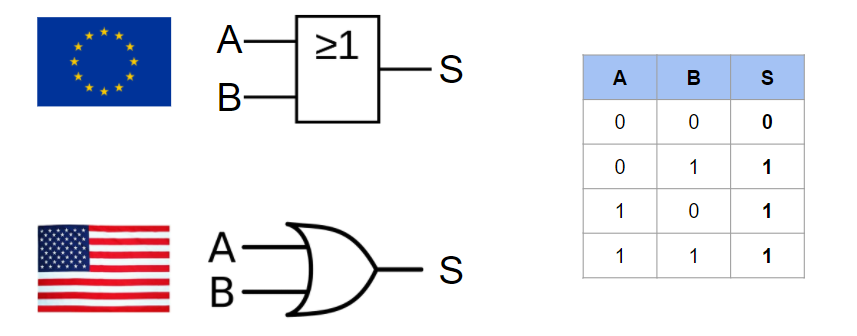
La porte logique XOR (ou exclusif)
La porte XOR est une porte OU exclusif, cela signifie que la sortie sera à ‘1’ seulement si un des bits d’entrée est exclusivement à ‘1’. Pour dire les choses autrement, cela correspond à une porte OR, sauf que la sortie es également à ‘0’ dans le cas ou les deux bits en entrée sont à ‘1’.
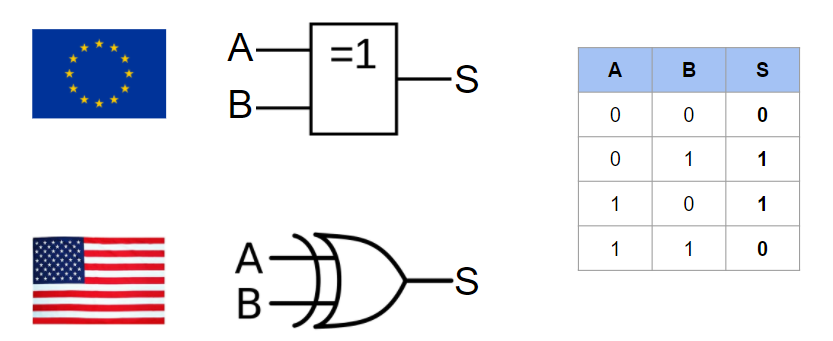
La porte logique NAND (non et)
La porte NAND pour “not and”, en français “non et”, porte mal son nom. En effet, cette porte correspond en fait à une porte AND suivie par une porte NOT. On retrouve alors en sortie, l’inverse de la porte AND.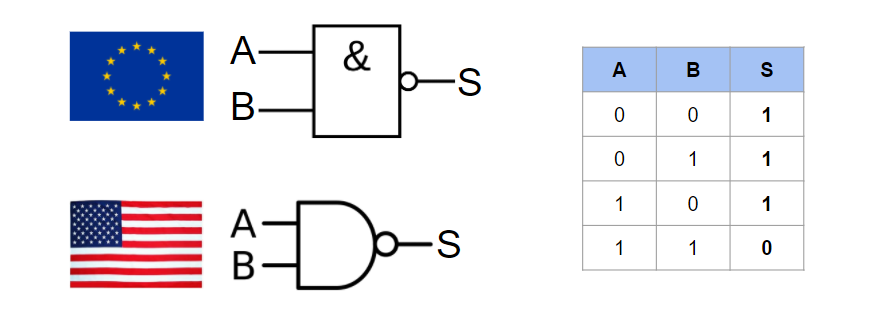
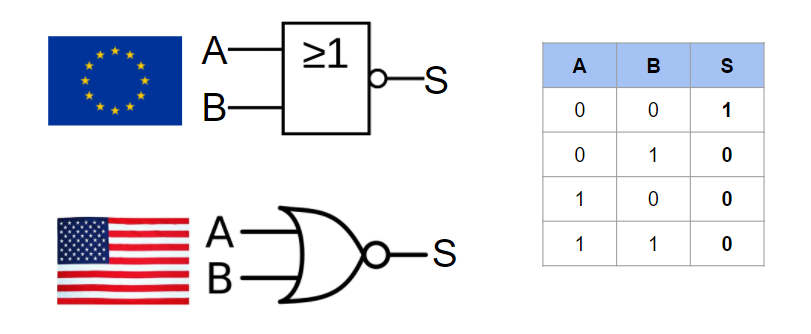
La porte logique NOR (non ou)
Comme pour la porte NAND, la porte NOR, correspond à l’inverse d’une porte OR.
Les circuits logiques
On appelle circuit logique l’assemblage de plusieurs portes logiques ensemble. Comme nous l’avons vue avec les portes logiques NADN et NOR, il est possible de représenter une porte logique comme étant la composition d’autres portes logiques.
Si on prend le cas de la porte NAND, elle correspond à une porte AND suivie par une porte NOT.
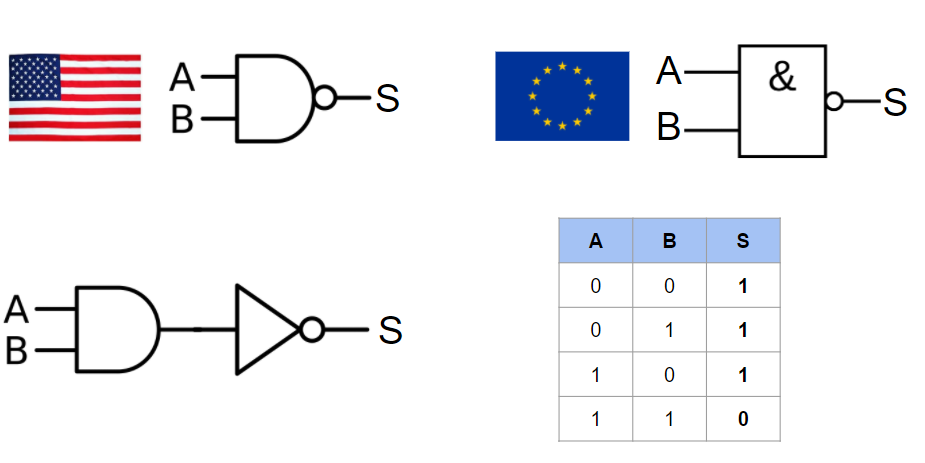
Il est alors possible de créer des circuits à partir de portes logique afin de réaliser des fonctions plus complexes. Prenons, pour la suite de l’article, l’exemple d’un additionneur.
Demi-additionneur binaire
Pour faire l’addition de deux bits, il est possible de créer un circuit logique. Il faut que ce circuit prenne en entrée les deux bits à additionner et qu’il génère en sortie la somme et la retenue. En effet, en binaire:
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 0 + (1 de retenue)
Pour réaliser ce circuit, on utilise alors deux portes logiques, une XOR (pour le somme) et une AND (pour la retenue).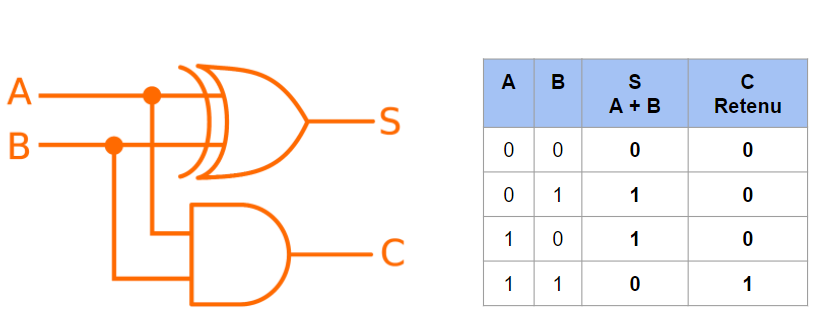
Attention, ici on parle de demi-additionneur car on ne prend pas en compte l’éventuelle retenu du bit précédent dans notre registre.
Additionneur binaire complet
Il faut ajouter une nouvelle entrée à notre demi-additionneur pour gérer la retenue du bit précédent et ainsi obtenir un additionneur complet.
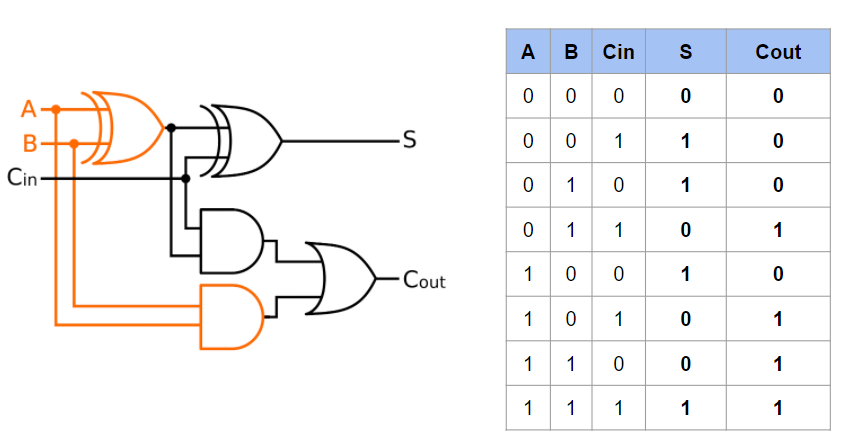
Pour avoir l’addition, on fait une première addition de nos deux bits (A et B), puis on additionne ce résultat avec la retenue du bit précédent (Cin).
Pour la retenu, on prend la retenue de A et B puis la retenue de (A+B) et Cin. Enfin on fait un simple OU sur ces deux valeurs pour obtenir notre retenue finale.
Additionneur de registres binaires
Bien, maintenant que l’on a un additionneur binaire complet, comment additionner un registre? Simplement en multipliant notre circuit par le nombre de bits constituant notre registre… Oui, cela risque de nous donner un circuit très complexe! C’est pour cela que l’on utilise une notion très importante en informatique: l’encapsulation.
l’encapsulation consiste a mettre dans une boite une fonctionnalité et d’en faire seulement sortir les entrées et sorties. Ainsi, l’utilisateur de la boite n’a pas à connaitre la composition interne de la boite pour l’utiliser. Cela simplifie alors grandement sont utilisation. On peux faire ici l’analogie avec le développement logiciel. On écrit ainsi des instructions qui seront encapsulées dans des fonctions, qui seront à leur tour encapsulés dans des librairies.
Encapsulons alors notre additionneur binaire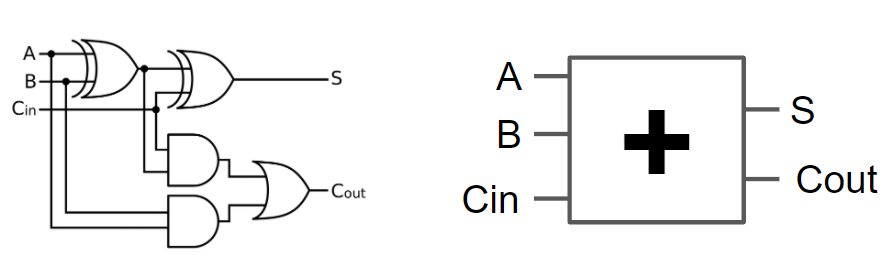
Maintenant, utilisons notre boite d’additionneur binaire pour faire notre additionneur de registre. On part ici sur un registre de 4 bits.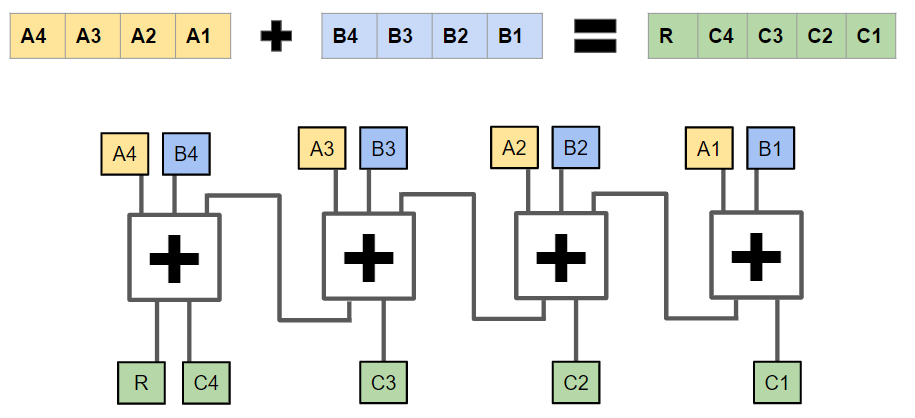
On prend bien ici la retenue de l’addition binaire précédente pour calculer l’addition binaire du bit courant.
Autres circuits de bases
Nous avons ici présenté l’additionneur mais il est possible de faire la même chose pour une soustraction, multiplication, …
Cela correspond à des instructions de base d’un processeur, au même titre que la comparaison de registre ou encore le décalage de bits dans un registre. Toutes les instructions de base d’un processeur sont ainsi constituées de circuits logique et donc par extension de portes logiques.