Vous avez surement déjà entendu dire qu’un ordinateur, ça fonctionne en binaire ou plus précisément avec des 0 et des 1. Mais finalement pourquoi? et surtout comment ça marche le binaire? Nous allons justement répondre à toutes ces questions cela dans cet article!
Le binaire en informatique
Lorsque votre processeur, qui est le cerveau du PC, vas traiter les instructions pour faire tourner vos programmes, il vas manipuler des 0 et des 1. De même, tout ce qui est stocké sur notre ordinateur est stocké sous forme binaire. Donc oui, vos photos, vos vidéos, vos fichiers texte, tout ce qui est sur votre ordinateur est en réalité représenté en mémoire par une suite de 0 et de 1.

On appelle cela le langage binaire ou en base 2 car il n’y a que 2 possibilités 0 ou 1. C’est le langage qu’utilise les différents composants de votre ordinateur pour communiquer entre eux et travailler.
A ce stade, vous allez vous dire que les développeurs sont vraiment des gens perchés et qui aiment se complexifier la vie. Et bien détrompez vous, un bon développeur est avant tout faignant ou plus exactement il cherche à faire des choses simples et efficaces. Le binaire est super simple et basique, il n’y a que 2 états 1 et 0, vrai ou faux
De plus si on regarde de quoi est constitué un processeur, par exemple, et bien vous allez voir qu’il est composé de plusieurs Milliards de transistors. Mais un transistor c’est quoi? et bien pour simplifier c’est une sorte d’interrupteur commandé électriquement. Quand il laisse passer le courant on dit que cela correspond au 1 alors que si le courant ne passe pas, cela correspond au 0. Il n’y a que deux états possibles ce qui correspond à notre bon vieux binaire.

Binaire et représentation
Bits et registres
Un élément qui permet de stoker des 1 et 0, s’appelle un BIT. Mais un BIT seul, n’est pas très intéressent, on les regroupes donc par paquet: les registres.
Un registre de 8 BITs correspond à un octet. Vous avez surement déjà entendu ce mot car c’est l’unité que l’on utilise pour la taille des fichiers sur un disque dure par exemple. À cette fin, on utilise couramment des multiples de l’octet, comme le kilooctet (ko), le mégaoctet (Mo), le gigaoctet (Go) ou le téraoctet (To).
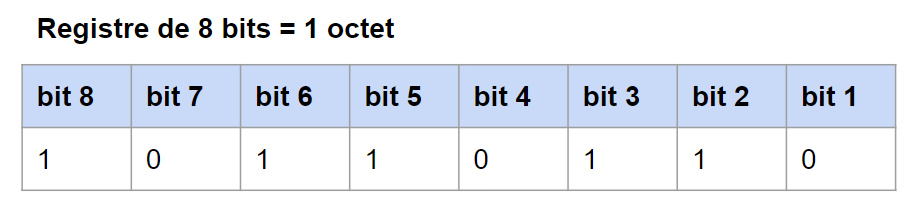
Le BIT de gauche est le poids fort et celui de droite le poids faible. Finalement c’est comme avec nos nombre décimaux, comme par exemple 123, ou le 1 est le digit de poids fort et le 3 celui de poids faible.
Décimale et binaire
Ok mais comment ça marche le binaire? pour bien comprendre, nous allons revoir un truc ultra basique mais vous allez voir que ça nous aidera a comprendre le fonctionnement du binaire. Dans la vie de tous les jours on compte en décimale ou base 10, cela signifie que l’on utilise 10 caractère différents pour représenter nos nombre. C’est clairement lié au fait que l’on a 10 doigts. On utilise donc les caractères 0 à 9 pour écrire nos différents nombre.
Cela vous parait surement logique et naturelle mais après tout, vous connaissez surement une autre représentation des nombres? Comme par exemple les nombres Romains.
Il se trouve qu’il existe en fait de nombreuses autre représentation des nombre comme par exemple le binaire (base 2), car ici on utilise uniquement 2 caractères pour représenter les nombre: 0 et 1
Représentation de nombres
Quand on représente un nombre en décimal, il arrive un moment ou nous n’avons plus assez de caractères différents. après le 9, il n’y a pas d’autre caractères. On augmente alors le nombre de digits pour représenter notre nombre et on joue avec les retenus. donc après 9, on reviens à 0 et on ajoute une retenu, ce qui donne 10.
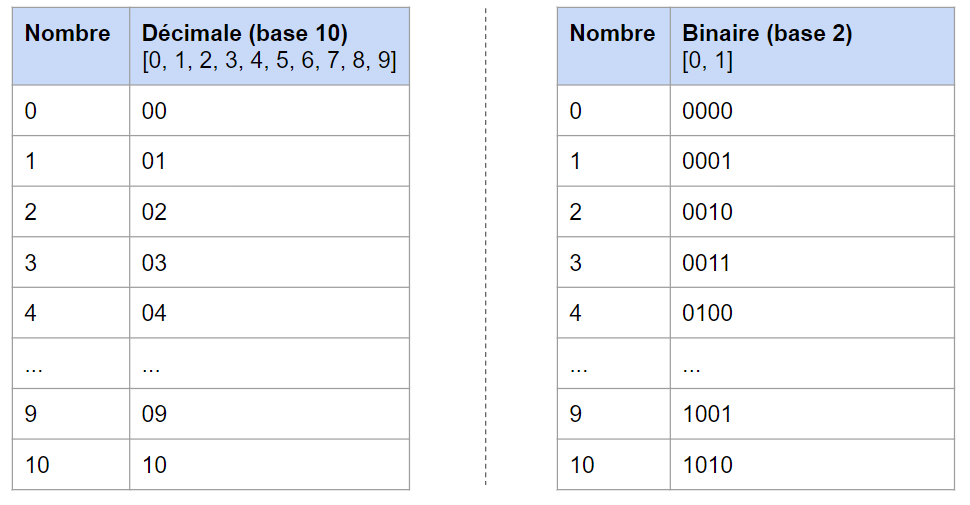
En binaire c’est le même fonctionnement mais ici, il n’y a que 2 caractères possibles. Pour le nombre 0, on utilise le caractère 0 et pour le nombre 1 le caractère 1. Mais pour le nombre 3 nous n’avons pas d’autres caractères, on reboucle alors tout en ajoutant une retenu. Pour le nombre 3 représenté en binaire, cela nous donne alors 10 (il faut lire ici ‘Un Zéro’ et non ‘Dix’).
Pour illustrer cela, voici une petite phrase célèbre dans le monde du binaire:
Il y a 10 types de personnes dans le monde : celles qui savent compter en binaire et les autres
Registre et poids des bits
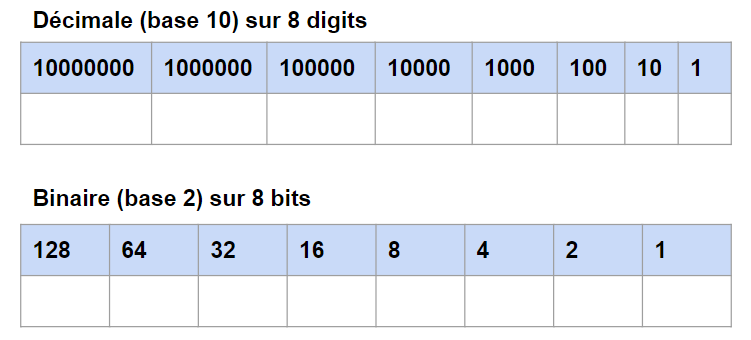
J’attire votre attention sur un point important avant de passer à la suite, comme pour le décimale et ses digits, en binaire nous attribuons des poids différents sur les bits de notre registre.
Par exemple pour le nombre décimale 123, cela correspond à 1*100 + 2*10 + 3*1 = 123
De même, en binaire, le nombre 1011 correspond à 1*8+0*4+1*2+1*1 = 11
Nous avons donc bien un poids différents pour chaque BIT, comme illustré dans le tableau suivant.
Il faut savoir qu’il existe de très nombreuses autres représentations, comme par exemple l’hexadécimale (base16) qui est aussi très utilisé dans le développement logiciel. Pour avoir 16 caractères différents, on prend les même que pour le décimale (0 à 9) et on ajoute à la suite les caractères A, B, C, D, E et F.
Binaire et conversion
Maintenant que nous avons vue comment représenter un nombre sous forme de binaire, voyons comment faire des conversions dans les deux sens.
Convertir un nombre binaire en décimale
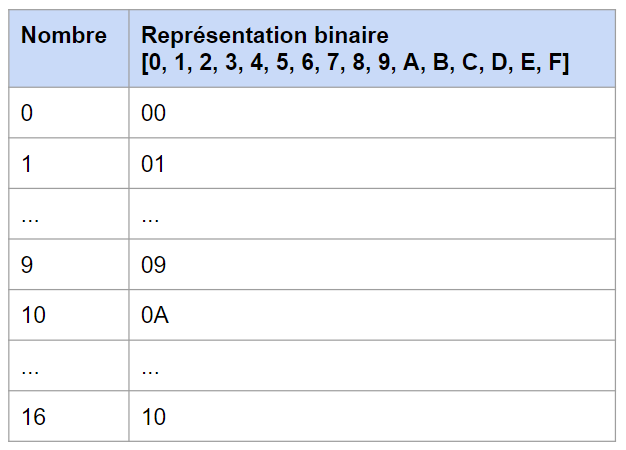
Pour convertir un nombre binaire ne décimale, c’est très simple. On prend les différents BITs que l’on multiplies avec leur poids, puis on en fait la somme. Par exemple pour cet octet: 10000010
1*128 + 0*64 + 0*32 + 0*16 +0*8 +0*4 +2*1 +0*1 = 130
Convertir un nombre décimale en binaire
Pour convertir un nombre décimale en binaire, nous allons également utiliser ce petit tableau avec les différents poids des BITs. Le principe est simple, imaginez que le nombre à convertir, correspond à un tas de billes. Le but est alors de remplir les cases du tableau avec les billes mais attention, il y a des règles:
- Il faut commencer par le BIT de poids fort et finir par celui de poids faible.
- Pour remplir une case, il faut mettre exactement le nombre de bille correspondant au poids du BIT.
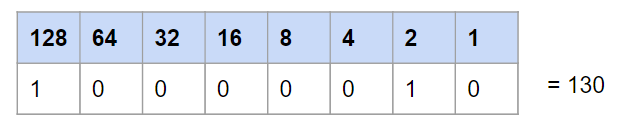
Prenons un exemple, le nombre 19, cela donne alors:
Avec 19 billes, je ne peux pas remplir complétement les case 128, 64 et 32. Je les laisses donc à 0. En revanche, je peux utiliser 16 de mes billes pour le BIT suivant. Je met un 1 dans la case et il me reste alors 3 billes. Je continue de la même manière jusqu’à ne plus avoir de billes.
Compter avec ses mains
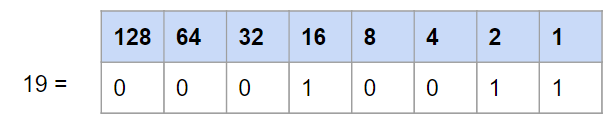
Vous savez déjà compter avec vos doigts…. mais vous comptez dans ce cas en décimale (base 10)! Voyons ensemble comment compter en binaire (base 2). Vous allez voir que c’est très puissant car cela nous permet de compter de 0 à 1023!
le principe est le suivant. vos 10 doigts correspondent à un registre de 10 BITs et donc un doigt est un BIT. Si il est baissé, c’est un 0 et si il est levé, c’est un 1.
 Par exemple pour représenter le nombre 513, on lève uniquement les deux pouces: Cela nous donne alors 10000 00001 = 512 + 1 = 513
Par exemple pour représenter le nombre 513, on lève uniquement les deux pouces: Cela nous donne alors 10000 00001 = 512 + 1 = 513
Utiliser des convertisseurs
Pour finir, vous pouvez utiliser des convertisseurs pour faire le travail à votre place. Vous pouvez utiliser des convertisseurs en ligne, ou encore la calculatrice Windows en mode programmeur.
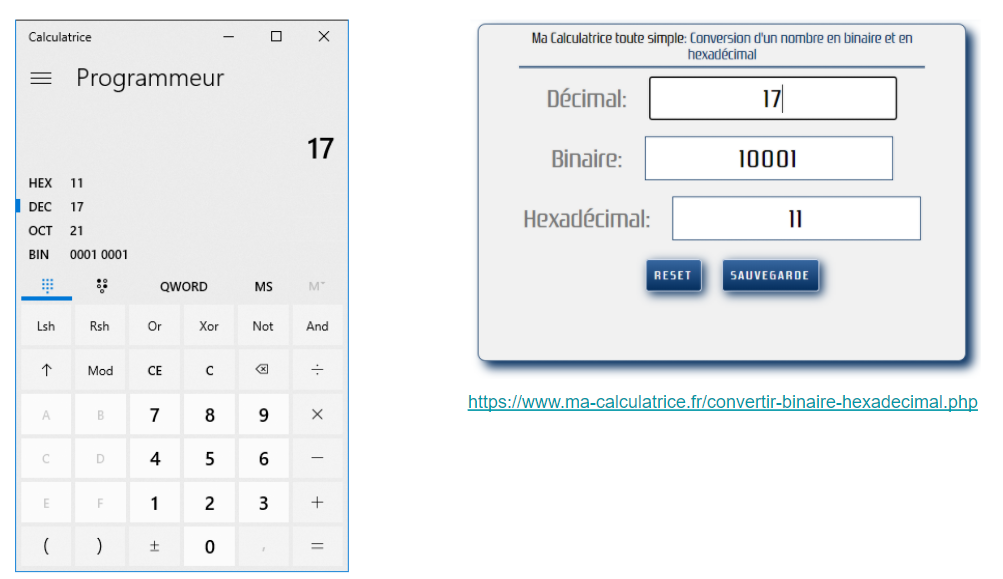
Cela vous permet d’écrire dans l’une des représentations et d’avoir instantanément la correspondance pour les autres représentations.
Binaire et codage
Vous vous demandez surement comment vous arrivez à regarder vos image ou encore à lire vos fichiers texte normalement si ils sont stockés sur votre ordinateur en binaire? Pourquoi vous ne voyez pas directement les 0 et 1?
Votre ordinateur utilise un “codage” pour interpréter les 0 et les 1 en une information utile comme une image ou un texte par exemple. Il existe une multitude de codage différents en fonction du type de données et même différents codage pour un même type. Par exemple les images, vous avez surement remarqué qu’il existe plusieurs extension (.jpg, .png, …), qui correspondent en fait à différents codage de l’information.
Dans le développement logiciel, il y a un codage très connu, c’est la table ASCII, qui permet d’interpréter des données binaire comme du texte. le fonctionnement est très simple. Il faut convertir des paquets de 8bits en un nombre décimale ou hexadécimale puis de prendre le caractère qui correspond dans la table suivante
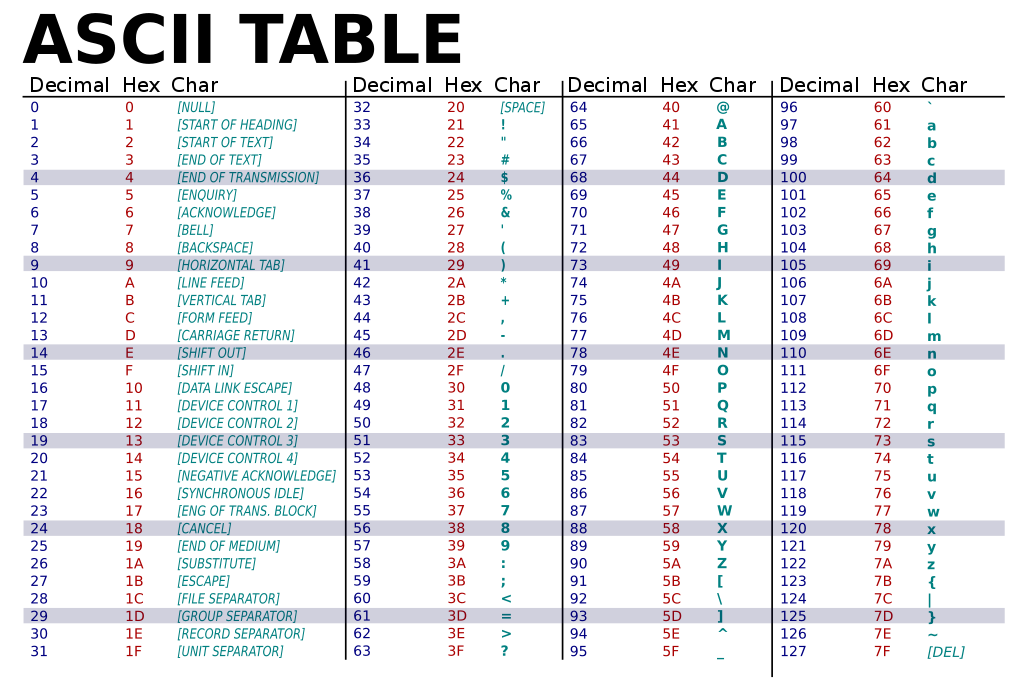
Prenons un exemple:
0100 1111 | 0100 1011
79 75
O K
Pour vous exercer voici un autre texte que je vous laisse décoder (indice: nom du site)
0100 0011 | 0110 1111 | 0110 0100 | 0111 0101 | 0111 0101 | 0111 0010 | 0010 1101 | 0101 0000 | 0111 0010 | 0110 1111
